裁剪中的初中数学
一年半前,开发了一个图片编辑器,里边的裁剪功能折磨的我死去活来。最近,裁剪这个需求又被搬了出来。再回头看那么久远的代码,果然全都忘了。就此重新找一下思路。
计算旋转后的裁剪框大小
最终效果如下:

具体到数学题就是,下图中黑色白色矩形的两个顶点位于黑色矩形的边上,黑色矩形的宽高比例与白色矩形的宽高比例相等,已知白色矩形的宽高和与黑色矩形的旋转角度,求黑色矩形的宽高。

这个问题一下把我带回了 2008 年,申奥成功都这么多年了,没想到我还得做几何题。不过仅凭着残余的一些数学知识,折腾了一会还是能勉强解出来的。
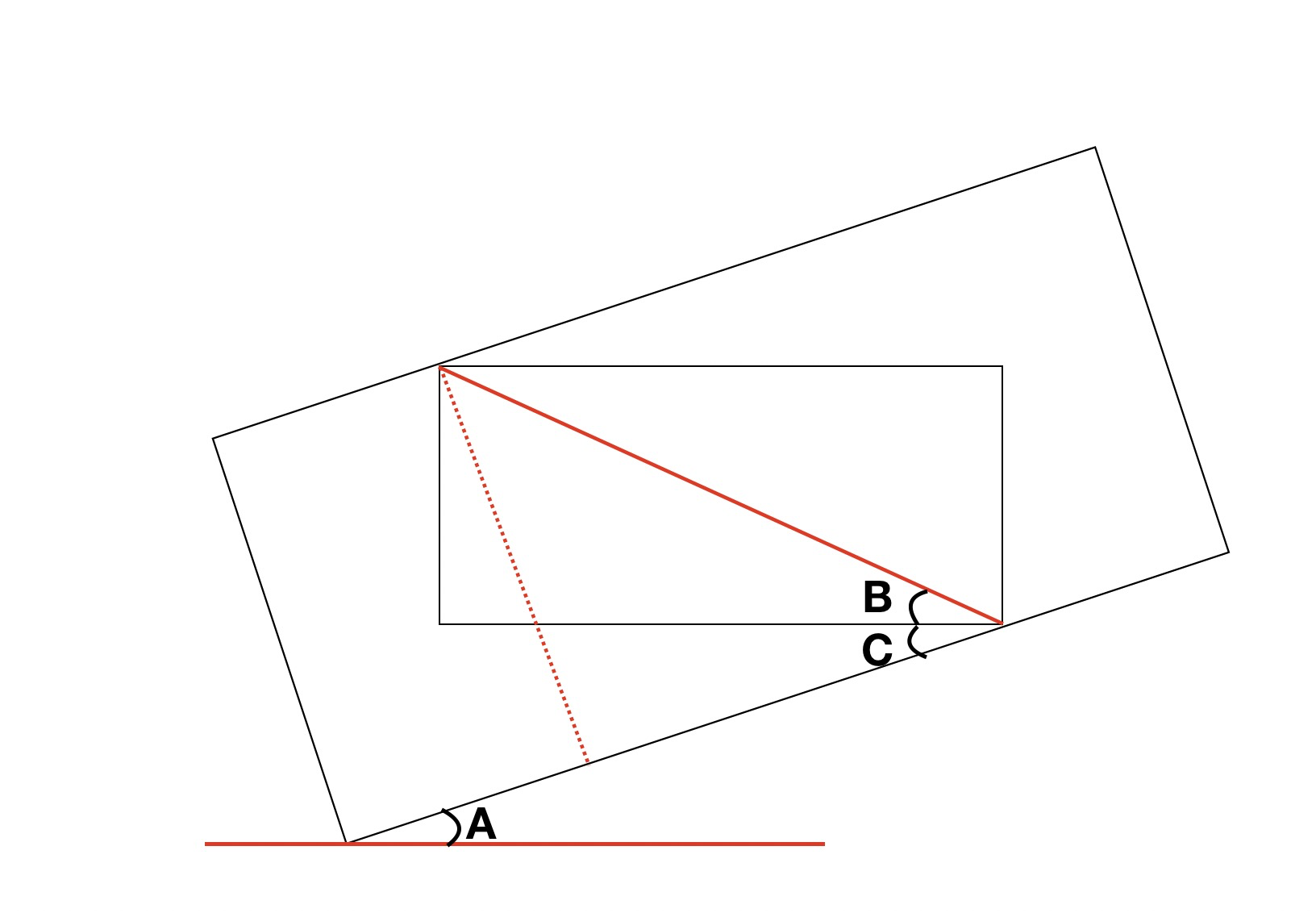
步骤如下:
- 已知内部矩形的宽高,可以求出角 B 的。
- 已知角 A 为旋转的角度。
- 因为角 C 与角 A 为互补角,所以角 C 等于 角 A。
- 作垂直于外部矩形一边的辅助线。
- 已知角 B 与角 C 以及内部矩形的斜边,所以可以求出辅助线的长度。
代码呢,就是这样:
1 | const getCropperRectSize = (innerRect, rotation) => { |
裁剪框拖拽后回弹
当把裁剪框拖拽出裁剪框并且松开鼠标鼠标后,它需要能够回弹到裁剪框内适当的位置,效果如下:

具体到数学题就是,已知大矩形 A 与小矩形 B,它们的宽高、旋转角度与位置信息都已知,求矩形 A 到矩形 B 内的最短路径。类似下图的情况:
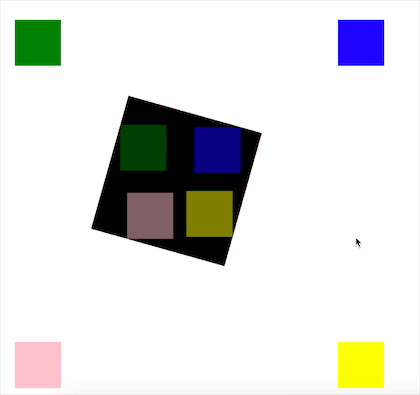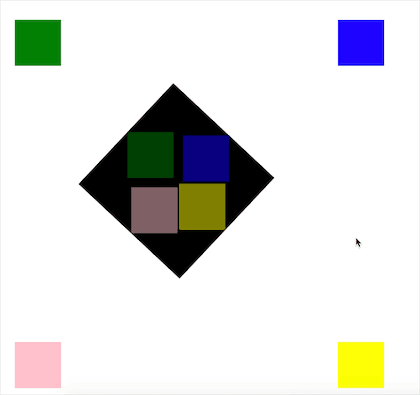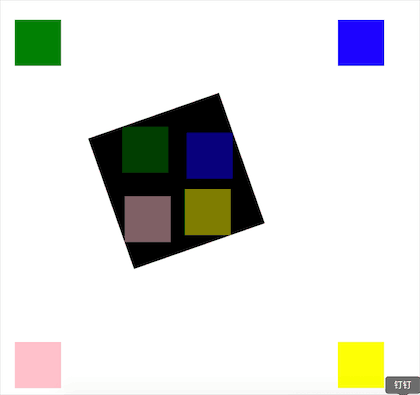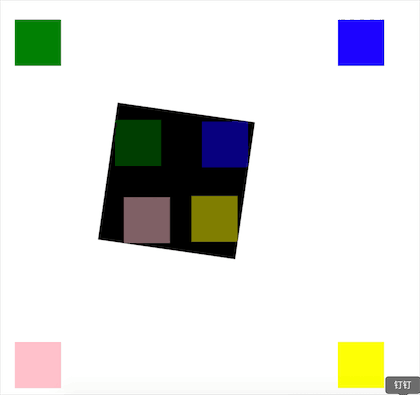
图中的黑色矩形即矩形 A,绿、蓝、粉、黄为四个矩形 B,它们在经过计算后的位置即黑色矩形内的四个对应颜色的矩形。
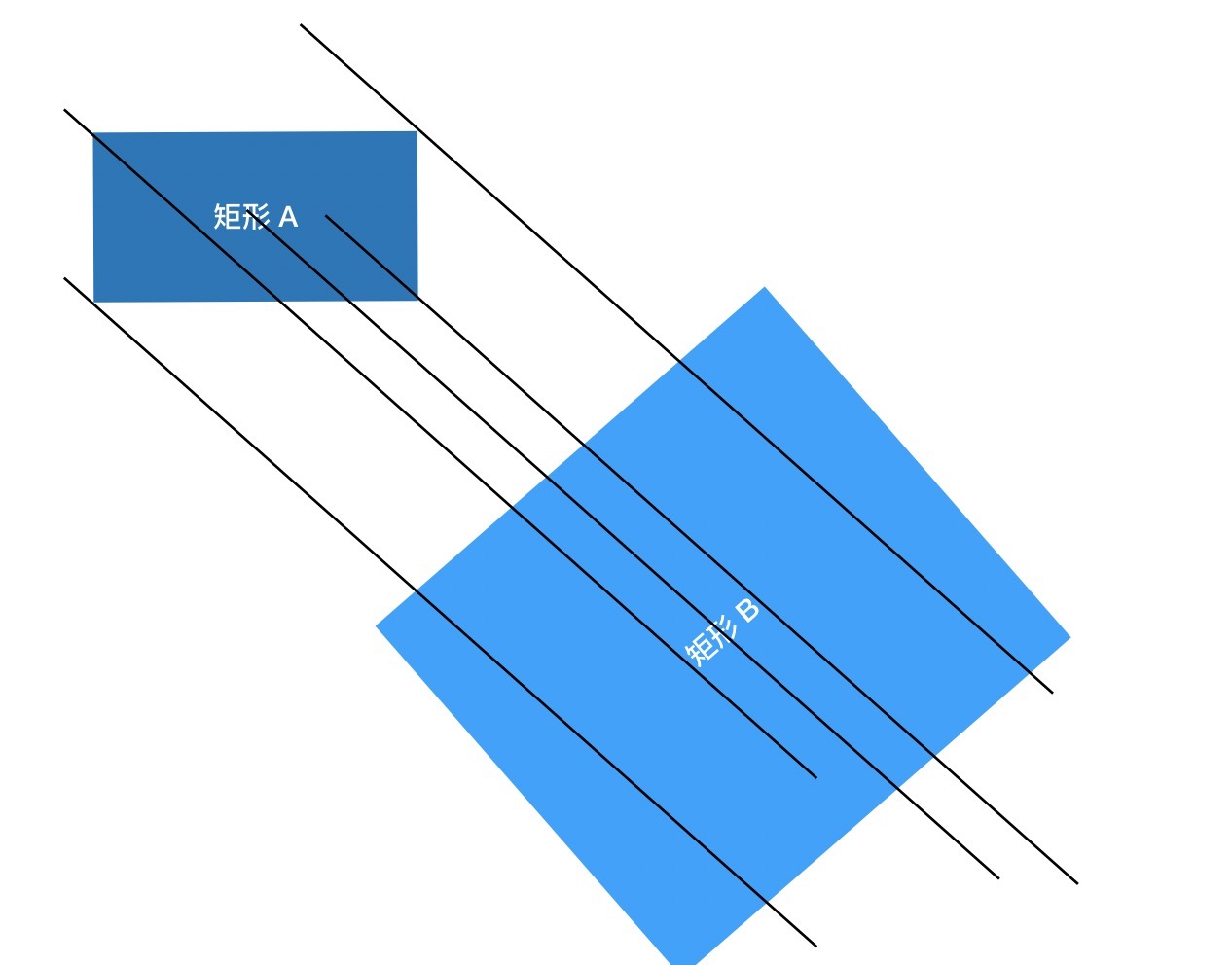
总体思路是:
- 作矩形 A 中点与矩形 B 中点的射线
- 过矩形 B 四个顶点作四条斜率与步骤 1 的射线相同的 4 条射线
- 对每条射线作一个顶点位于射线与矩形 A 的交点上的矩形
- 这些矩形中位于矩形 A 中过的即符合规则的矩形
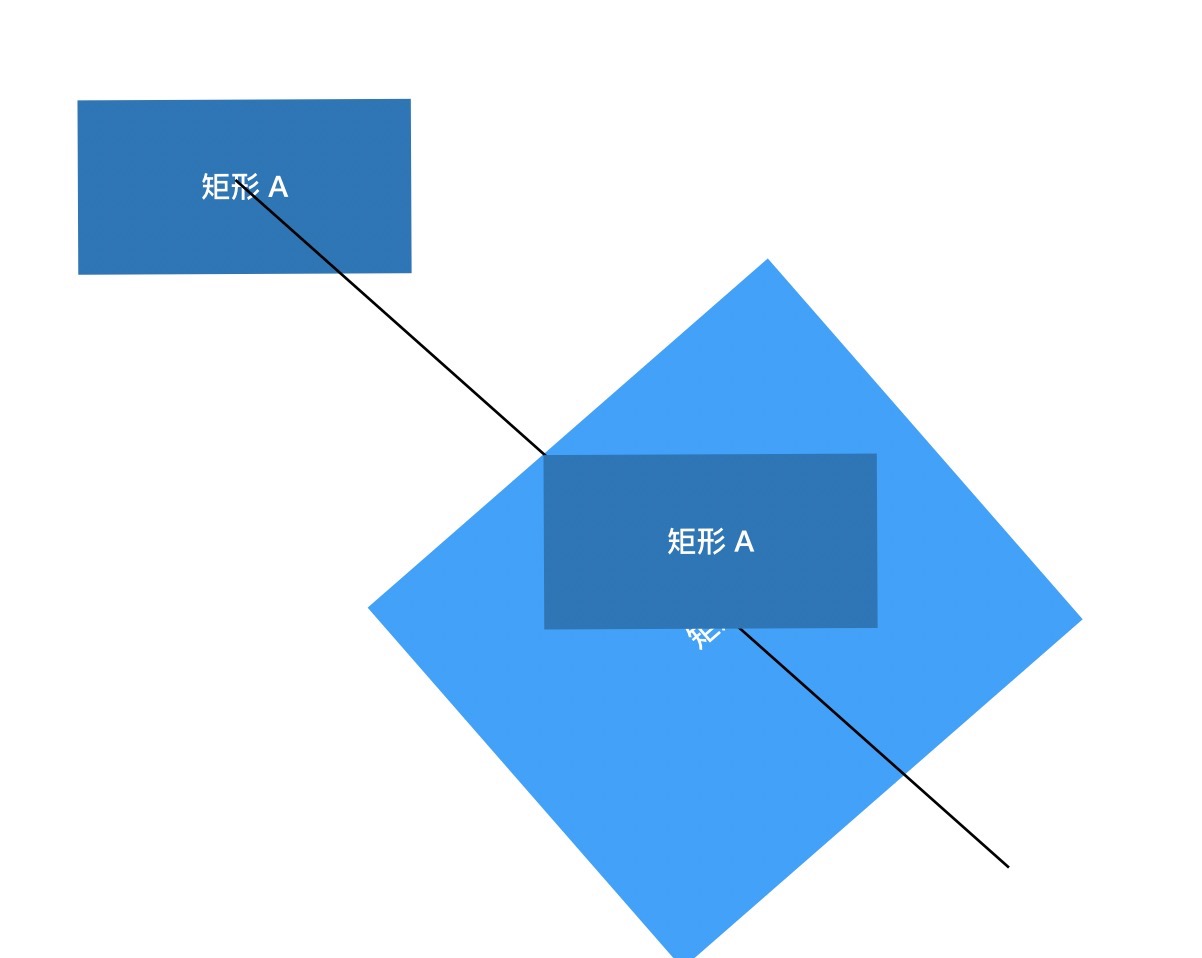
最后,2020 年了,愿以后的工作中没有数学。